EvoMath 2: Testing for Hardy-Weinberg Equilibrium
In the first installment of EvoMath, I derived the Hardy-Weinberg Principle and discussed its significance to biology. In the second installment I will demonstrate how to test if a population deviates from Hardy-Weinberg equilibrium.
Recap:
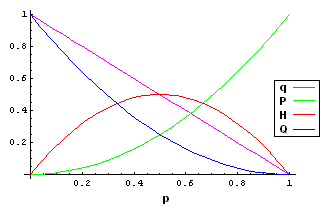
A population is considered to be in Hardy-Weinberg equilibrium if the allele and genotype frequencies are as follows.
| Genotype | Frequency |
| AA | \(P = P^\prime = p^2\) |
| Aa | \(H = H^\prime = 2pq\) |
| aa | \(Q = Q^\prime = q^2\) |
| Allele | Frequency |
| A | \(p = P + \frac{H}{2}\) |
| a | \(q = 1-p = Q + \frac{H}{2}\) |
Test Procedure:
A goodness-of-fit test can be used to determine if a population is significantly different from the expections of Hardy-Weinberg equilibrium. If we have a series of genotype counts from a population, then we can compare these counts to the ones predicted by the Hardy-Weinberg model. We conclude that the population is not in Hardy-Weinberg equilibrium if the probability that the counts were drawn under the Hardy-Weinberg model is too small for the deviations to be considered due to random chance. The significance level that is typically used is \(\alpha = 0.05\), i.e. the genotype counts have less than a one in twenty chance of being caused by a population in Hardy-Weinberg equilibrium.
In order to calculate this probability, we will use a test statistic, \(\chi^2\), which was devised in 1900 by Karl Pearson and has a well characterized distribution. If \(O_i\) are the set of observed counts, and \(E_i\) are the set of expected counts, then
\[\chi^2 = \sum_i{\frac{ \left( O_i-E_i \right)^2 }{ E_i }}.\]This test statistic has a “chi-square” distribution with \(\nu\) degrees of freedom. Since we are testing Hardy-Weinberg equilibrium with two alleles, \(\nu=1\) (rationale not shown). Furthermore, it can be shown that if \(\chi^2 \ge 3.841\) then \(\Pr{ \left\{ \chi^2 \right\} } \le 0.05\). Therefore, if \(\chi^2 \ge 3.841\) we will reject the null model and conclude that there is significant statistical support that the population is not in Hardy-Weinberg equilibrium.
Example 1:
Consider the following samples from a population.
| Genotype | Count |
| AA | 30 |
| Aa | 55 |
| aa | 15 |
| Allele | Frequency |
| A | 0.575 |
| a | 0.425 |
Calculate the \(\chi^2\) value.
| Genotype | Observed | Expected | (O-E)2/E |
| AA | 30 | 33 | 0.27 |
| Aa | 55 | 49 | 0.73 |
| aa | 25 | 18 | 0.50 |
| Total | 100 | 100 | 1.50 |
Since \(\chi^2 = 1.50 < 3.841\), we conclude that the genotype frequencies in this population are not significantly different than what would be expected if the population is in Hardy-Weinberg equilibrium.
Example 2:
Race and Sanger (1975) determined the blood groups of 1000 Britons as follows (from Hartl and Clarke 1997).
| Genotype | Observed | Expected |
| MM | 298 | 294.3 |
| MN | 489 | 496.4 |
| NN | 213 | 209.3 |
This results in \(\chi^2 = 0.222 < 3.841\). As in the previous example, the measured genotype frequencies are not significantly different from the expectations of Hardy-Weinberg equilibrium.
Example 3:
Matthijis et al. (1998) surveyed a group of 54 people suffering from Jaeken syndrome (from Freeman and Herron 2004).
| Genotype | Observed | Expected |
| OO | 11 | 19.44 |
| OR | 43 | 25.92 |
| RR | 0 | 8.64 |
This results in \(\chi^2 = 23.56 > 3.841\). Unlike the previous two examples, the measured genotype frequencies are significantly different from the expectations of Hardy-Weinberg equilibrium. This indicates that one or more of the Hardy-Weinberg conditions are being violated; although, it does not tell us which ones.
Conclusion:
Although to derive the Hardy-Weinberg principle, we assumed that the size of the population was infinite, these statistical tests demonstrate that finite populations can approximately exist in Hardy-Weinberg equilibrium.
- Freeman S and Herron JC (2004) Evolutionary Analysis 3rd ed. Pearson Education, Inc (Upper Saddle River, NJ)
- Hartl DL and Clarke AG (1997) Principles of Population Genetics 3rd ed. Sinauer Associates, Inc (Sutherland, MA)
- Matthijis GE et al. (1998) Lack of homozygotes for the most frequent disease allele in carbohydrate-deficient-glycoprotein syndrome type 1A. American Journal of Human Genetics 62: 542-550
- Race RR and Sanger R (1975) Blood Groups in Man 6th ed. JB Lippincott, Philadelphia
