Weasles on Parade
It is now 62 hours since William Dembski posted that the Evolutionary Informatics lab was going to try and reproduce Dawkins Weasel Program according to how it was actually written, as opposed to their fantasy version. In that time I’ve resurrected an elderly program, and several readers have made their own weasels from scratch. Commenter Anders has even made a Python version that puts “freely mutating” and “locking versions” head to head with great graphs. (Update: Wes Elsberry did a head to head comparison last year, see here for his comparison [scroll down], it differs from my implementation but the basic message is the same).
I’ve gone back and done a head to head comparison myself between a program with no “locking” (all letters in any given string have a chance to be mutated) and one with “locking” (where the matching letters are preserved against mutation). Trying to implement “locking” al la Dembski proved too hard. You have to keep indices of the letter locations and keep updating them. It is such a pain in the bottom to try and do this that I cannot imagine Dawkins even wanting to try and program a “Locking” implementation in GBASIC. Remember, Dawkins weasel was a quick and dirty program bashed out in a short time. To implement “locking” I just kept a copy of the parent string unmutated (after all, in the real world not every offspring has mutations in genes of interest).
So what happened?
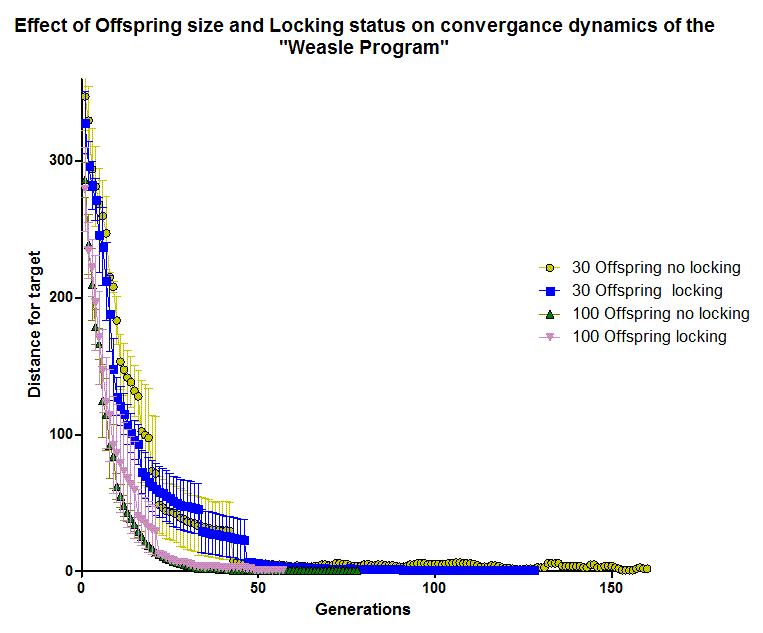
As you can see they were much the same (mean and standard error of an average of 4 independent runs per condition shown, click to embiggen). “Locked” runs finished earlier, on average but most of the trajectory of the run was determined by mutation supply. As you can see, runs done with locked and unlocked versions fell within the error bars of each other, for runs that set the Offspring number at either 100 or 30.
This is easy to understand. Early on, virtually any mutation is of big benefit, while later on most mutations are of small benefit. Only in the final stages that there was any significant backing and forthing, and then only in the 30 Offspring case. In the 100 offspring case, the population was so large that the probability was high that even in the final stages a beneficial mutation would be acquired. Wesley Elsberry has done the mathematics explicitly (go to this link and scroll down). Only in the 30 offspring case was the last 10 or so generations in an “unlocked” run spent bouncing from 3-1 differences.
So Dembski’s claims that a list of every 10th output string shows that Dawkins is using a “locking” program are nonsense, Dawkins results are exactly what we would expect to see when sampling sparsely from a high population “freely mutating” weasel run.
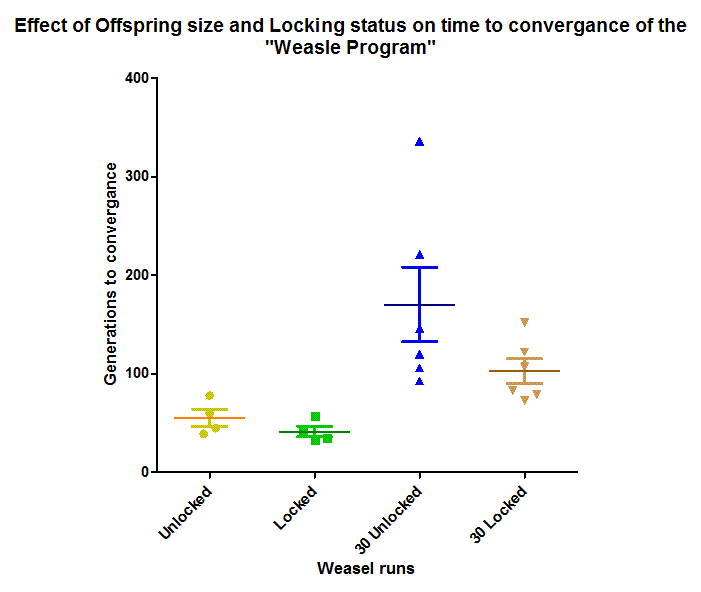
Slightly more surprisingly, the median time to convergence (when the program finally reached the target string), was not actually statistically significantly different. I suspect when enough runs are accumulated (say around 20), they will be, but the “locked” runs are only about 20% faster.
So, summary. Whether you “lock” your strings, or allow them to mutate at all positions freely, a weasel program will converge on a solution. The for most of the time, mutation supply dominates, and whether you lock your strings or not there is rapid accumulation of beneficial mutations. Only at the very end run does “locking” matter, and then only for small populations where the probability of a beneficial mutation is low.
But even then, “unlocked”, freely mutating programs will converge on a solution in less than a minute (and only 20% slower than the “locking” programs), when simple random sampling will take longer than the lifespan of the Universe to converge.
Still, the point is that against all evidence, Dembski believes that Dawkins wrote a overly complicated program in GBASIC, and then reverted to a simple one for a TV show, and can’t be bothered to get around to writing the code that would show him wrong (and show that freely mutating programs converge rapidly on the target string). Again, this shows that cdesign proponetists don’t understand the “test your hypothesis” part of science. I’m currently reading Galileo’s “Starry Messenger”, and the debate over at Uncommon Descent reminds me of Francesco Sizzi, who declared that Galileo really couldn’t have seen Moons around Jupiter, as metaphysics demands there only be 7 planets.
Now If only they would put the same degree of effort that they put into critiquing the weasel program, a toy demonstration of selection the same importance as the measuring cylinder/running tap model of drug clearance, into doing some real science.
The freely mutating QBASIC program is here, the “locked” version is here (both write strings to a log file).
Feel free to submit your own weasels, especially ones that compare freely mutating vs “locking” versions of the code, and the PT crew could do with a java applet version if you could do one. A weasel for every 6 hours the Uncommon Descent people do nothing would be great!
See Wesley Elsberries superb Java Weasel as an example!