Mapping fitness: landscapes, topographic maps, and Seattle
The concept of a "fitness landscape" is a fundamental idea in evolutionary biology, first introduced and established during the so-called "evolutionary synthesis" in the early 20th century. It was the great Sewall Wright who pictured adaptation as a "walk" through a landscape (pictured below), where the walking is done by variants (of an organism or a molecule) and the landscape is a theoretical representation of the relative fitness of the variants. (J.B.S. Haldane did similar work around the same time, but Wright's paper is much better known perhaps because it's more accessible to non-experts. See Carneiro and Hartl in PNAS earlier this year for more.)
It's a simple concept, and a helpful one, though sometimes subject to over-interpretation. And it helps to frame some of the big questions in evolutionary genetics. One of those big questions is this one, stated somewhat simplistically: how do the variants navigate to fitness peaks, if there are fitness valleys that separate the peaks? (The ideas is that fitness is higher on the peaks, and so a population would be unlikely to descend from a local peak into a valley.) In other words, given a particular fitness landscape, what are the evolutionary trajectories by which variation can explore that landscape?
Such a question calls out for an experiment. It would be so nice to be able to map fitness landscapes using hard data, so as to design and perform experiments on the navigation of adaptive walks. Specifically, this would facilitate an empirical examination of the genetic structure underlying the fitness landscape, and that's how a lot of the interesting questions about evolutionary exploration will be addressed. Of course, biologists have been working on this for a long time, and we've learned a lot about real fitness landscapes over the decades. But detailed maps of such landscapes require detailed knowledge of the genetics of the landscape, and that has presented a significant technical challenge. Because of these technical limitations, examination of fitness landscapes have been either highly focused on very small landscapes (say, the fitness of a small number of variants) or have described the landscapes at very low resolution (by analyzing a tiny subset of the possible variants).
It's worth taking some time to understand the problem before we look at how new techniques and approaches are changing the situation.
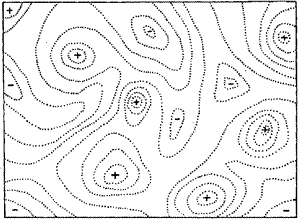
Look at Wright's drawing. It looks like a topographical (topo) map, with dotted lines indicating parts of the landscape that represent equal fitness. And it looks smooth, like a topo map of rolling hills or dunes. The elevations represent fitness, but what do the lateral distances represent? They represent variation: more specifically, each point on the map represents one particular genetic variant. It doesn't matter whether we're talking about a whole genome navigating a complex fitness landscape or a single protein navigating a map of one specific function. Either way, each point on the map is a different variant. And, importantly, each point on the map is adjacent to many other points on the map, such that a tiny change (a single nucleotide change in a DNA sequence, for example) results in a step from one point to an adjacent point. This means that a map like Wright's is likely to depict the postulated fitness of enormous numbers of variants: even a seemingly simple map of the function of one molecule, in order to be a complete map, would have to account for millions of potential variants. (For example, an average-sized protein composed of 400 amino acids can be made 20400 different ways.) Even if the map only seeks to account for the function of a small part of a protein, say, 10 amino acids, that's still 2010 different possibilities. That's a lot of possibilities.
And that's a problem for at least one reason. Wright's map shows a smooth landscape, in which changes in fitness happen in small increments as the variants diverge from each other. His map creates the impression that closely-related variants will differ only slightly in fitness from each other. But reality could be completely different in a given case. It could be that the real landscape is a crazy cacophony of varying fitnesses, with an aerial topography more like downtown Manhattan than like the dunes of West Michigan. And it could be a mixture of both: smoothly varying overall topography that arises from more dramatically varying local topography.
To tackle such a problem, we would need to be able to measure the fitness of zillions of variants, in such a way as to be able to link the fitness measurement to the exact genetic makeup of each variant. In more technical terms, we need to describe/measure phenotypes of zillions of genotypes, and we need to know both the phenotype and the genotype of each of those zillions of variants. How can this be accomplished, or is it even possible?
Three recent papers serve as excellent examples of how scientists are working on questions like this. One notable thing about the papers is, of course, the fact that they have tackled this seemingly intractable problem. Another is the technological advance (next-generation DNA/RNA sequencing) that largely explains the breakthrough success of two of the research groups. And another is the fact that all three labs are located in one particular metropolitan area, an area that is home to an anti-scientific think tank that claims to be interested in the very same questions.
We'll explore those three papers in three subsequent posts. But if you want to get started now, here are the articles to read:
Optimization of DNA polymerase mutation rates during bacterial evolution. Loh et al., PNAS.
High-resolution mapping of protein sequence-function relationships. Fowler et al., Nature Methods.
Rapid Construction of Empirical RNA Fitness Landscapes. Pitt and Ferré-D'Amaré, Science.
(Cross-posted at Quintessence of Dust.)
