Calling ID's Bluff, Calling ID's Bluff...
In July, I described a Genetic Algorithm that, unlike Dawkins’ “Weasel” experiment, specifies no fixed “Target” for the simulation, but instead rewards those members of the current population which use fewer or shorter segments to connect a fixed set of points. As the algorithm progresses, it finds a multitude of answers for the math problem called “Minimization of Steiner Trees,” i.e. the shortest possible straight-line networks connecting the fixed points.
Last Monday, I posted Take the Design Challenge, wherein I called for solutions to a tricky little 6-point network. Next Monday, I will announce the winners (there are 20 entries already, several with true Steiner Solutions, and others with almost-as-good “MacGyver” solutions).
Imagine my surprise, then, when I found Salvador Cordova at Uncommon Descent spewing blatant falsehoods about this work. I was shocked - shocked, I say - to catch the UD Software Engineers in a lie. And quite a lie it is - with the help of mathematicians like Carl Gauss, I’m going to lift the veil from the obfuscations of IDers, and prove it’s a Lie, much as you would prove a mathematical theorem.
In his reply to the Design Challenge, Mr. Cordova describes a genetic algorithm of his own devising, for solving the problem of adding up all the integers from 1 to, say, 1000. (The result is 500,500, by the way). Cordova writes
The following computational theatrics are akin to what Dave Thomas performed:
and then links to his GA code, here.
Salvador adds later in his post that
ofro wrote: What I don’t understand is the basic premise of your example, which apparently already has an explicit solution of the problem built into the program.
I’m afraid that isn’t quite correct because if you go to ga.c, and do a text search for 500500 you won’t find it. The solution was never explicitly stored anywhere.
It seems Sal is implying that his sum-of-integers genetic algorithm has no “fixed target,” and is akin to my work on Steiner Trees.
That is patently False. Cordova’s algorithm is exactly like Dawkins’ “Weasel”, with the major difference being that, while Dawkins was searching for the specific target “METHINKS IT IS LIKE A WEASEL,” Cordova is searching for the specific sequence of numbers 251, 252, 253, … 750. When these are summed and doubled, the result is the sum of the numbers from 1 to 1000: 500,500.
Another oddity was that Cordova’s code wouldn’t even compile – it took me a couple of hours to reverse engineer it and figure out what in tarnation he was doing. As an exercise in Smoke and Mirrors, Cordova’s algorithm is remarkable. But, unlike my program, it is definitely looking for one, and only one, Answer.
PROOF
Cordova’s program loops from 1 through half the desired end-number; if the sum of the first N integers is desired, and N=1000 (as in Cordova’s listing), then he loops from 1, 2, 3, up to 500 (=N/2).
For each of the 500 numbers, Cordova stores a number that represents a “Midpoint Distance” (I’ll call this MidPoint[i] for short, where i is any number in the sequence 1, 2, 3, … N/2.)
Initially, his Midpoint Distances are generated randomly, with values anywhere from -2N to +2N (e.g. -2000 to +2000). Then, he loops through each of the N/2 numbers once per generation, and repeats the process over many generations. For a given generation, and a given looping number from that generation (such as i=37, with value MidPoint[37]), Cordova calculates a “pseudo-euclidean distance”:
double pseudo_euclidian_distance( double x1, double x2, double y) { return (x1-y) * (x1-y) + (x2-y)*(x2-y); }
Here’s how he uses this distance. At each step in the loop (from 1 to N/2), the “distance” to the current MidPoint value is examined, and a “mutated” MidPoint distance is also derived, always within a few units (plus or minus 2.5) of the original “distance”. If the Mutated “distance” is shorter, that distance then replaces the current value, MidPoint[i]. Otherwise, the current value is retained. So, something is definitely being minimized, but what?
Aside: if you think this exposition is getting too wordy, please do try to figure out Cordova’s Code for yourself. I’ll wager you’ll be back here before you know it!
If the pseudo-Euclidean distance is called D, then Cordova is trying to minimize D = (x1-y)^2 + (x2-y)^2. To see where this will lead, one can take the derivative of D with respect to y, and set it to zero to find the extremum (which is indeed a minimum, but I’ll leave that detail to the reader):
D’ = 2 (x1-y)(-1) + 2(x2-y)(-1) === 0, => (x1-y) + (x2-y) === 0, => y = (x1 + x2)/2.
Whatever x1 and x2 are, Cordova’s function will be minimized when the value of y (which turns out to be a MidPoint value) equals the average of x1 and x2.
Delving deeper into Sal’s Nightmare, one finds that, if you are on the ith number in the loop (say, i = 37), what gets sent down as x1 and x2 are just the index i itself, and that same index + N/2. Thus, for i=37, it turns out that x1 = 37, and x2 = 537. Not coincidentally, the average of 37 and 537 is 287, or simply 37 + 250.
And that’s almost all there is to it. Even if the value for the 37th midpoint was far off at the beginning (say, -1634), as the generations proceed, any mutations that serve to bring the midpoint closer to the intended value (=287) are accepted, and those that don’t are rejected.
Formally substituting i for x1, and i+N/2 for x2, we see that midpoints are drawn inexorably to the value y = (x1 + x2)/2 = (i + i + N/2)/2 = (2i + N/2)/2 = i + N/4.
If N is 1000, N/4 is 250. The first midpoint (for loop index i=1) is drawn to 251 (=1 + 250), while the 37th midpoint is drawn to 287 (=37 + 250), and the final index’s midpoint is drawn to 750 (=500 + 250).
All that remains is to evaluate the final “estimate,” which is just the sum of the 500 (or N/2) midpoints, doubled.
Here follows the proof that this sum is just a roundabout way of calculating the sum of the first N integers, which the brilliant Gauss found useful as a child to escape some boring math drills: instead of adding the numbers up, Gauss realized the sum of the first N numbers was just (N*(N+1)/2).
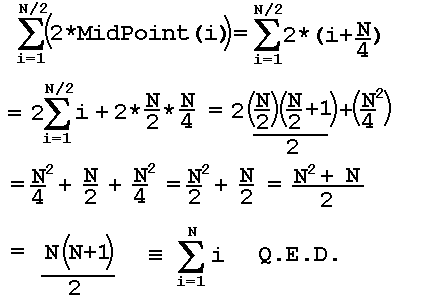
And that’s that. Unlike the normal he-said/she-said arguments, this disagreement boils down to basic Math.
The Software Engineering Team of Uncommon Descent has been caught lying - Q.E.D.
