Does approach to higher probability block natural selection?

In his video, which we have discussed ad nauseam in our extremely long recent thread Mark Champneys claims that scientists are ignoring science when they claim that natural selection can result in functional information increasing in the genome. In the subsequent discussion, Champneys insisted that there was a generalized form of the Second Law which made such increase impossible, insisted that it applied not just to isolated systems but to non-isolated populations of organisms, and that it did prevent natural selection from achieving long-term improvement.

In this post, I hope to show a very simple example, and to get away from the issue of whether this has anything to do with the Second Law. If we can focus on discussing whether the approach of a stochastic process to its equilibrium prevents natural selection from having effect, maybe we can avoid having 1,600-plus comments and actually discuss the matter at hand.

Let's try for that focus and relevance. Surely someone who wants scientists to actually grapple with the science must agree with that goal. Right? Let's see ...

The example

My simple example will be a large population of organisms, haploid ones, for simplicity. We will follow 100 sites in their DNA. At each site there are four possible bases, A, C, G and T. There will be a simple mutational process which changes symmetrically among the four possible bases (technically, a Jukes-Cantor model of change). Each base has the same probability of mutating, and when it mutates it changes to one of the other three bases, chosen at random. We'll take the probability of mutation to be 0.0001 per base per generation, a fairly high value. No matter what the population of sequences is, as mutations accumulate, the population proceeds towards its equilibrium. Each site becomes equally likely to have all four bases, and this happens independently at all 100 sites. The equilibrium has all 4^(100) possible sequences, equally frequent. If we were to follow only how many copies of one of the four bases, say C, the sequence has, each site has a 25% chance of having a C. So on average there will be 25 Cs. It will be like coin tosses of a biased coin, with 100 tosses, on average 25% of which are Heads. This is a binomial distribution. In the figure above, it is the orange histogram, which varies around 25. If having lots of Cs were somehow desirable, with only mutation, the sequences are stuck in the vicinity of 25, forever.

The process of change of these sequences is a random process (a stochastic process), and it has a single equilibrium distribution toward which it proceeds. In technical terminology, this is an ergodic process. So far things look as if they follow Mark Champneys' rules.

With natural selection

But notice what is left out -- natural selection. So let's consider another case, which puts it in. Suppose that at a site, having a C improves the fitness of the individual by 0.005, which is one part in 200, or 0.5%. And suppose that this happens at all the sites. For simplicity we'll suppose that the higher fitness is always for C, with all three other bases having the equal, slightly lower fitness. The fitnesses at the different sites combine by multiplying. So the fitness of a 100-base genotype is 1.005, raised to the power of the number of Cs in those sites.

It will not be a big surprise that Cs increase at each of the sites. I'll leave out the algebra, but can supply it on request. Starting out with a population gene frequency of 0.25 at all 100 sites, the gene frequencies are always the same at all of the sites, but they rise gradually. After about 5,000 generations. they rise almost to 1, settling in to an equilibrium gene frequency of 0.9801332. They don't get all the way to 1, because mutation has continued, and Cs keep mutating away from C as well as being selected towards it.

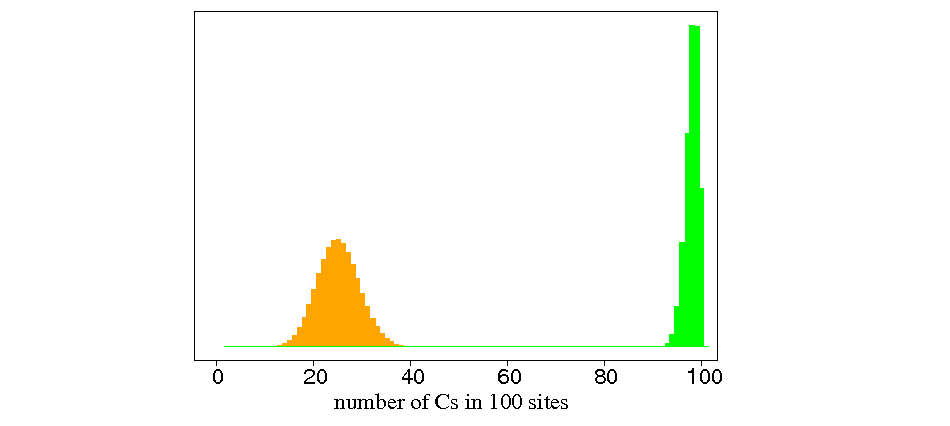
In the figure, the result is the green histogram. There are an average of 98.01332 Cs in these 100 sites. The number varies around that from genome to genome, just as tosses of 100 coins would that have a Heads probability of 0.9801332. It is possible to show that the average fitness of genomes in that equilibrium distribution is 1.630472. Natural selection shifts the equilibrium distribution dramatically to the right.

Mark Champneys is right (and also wrong)

Yes, in both of these cases the random process results in an equilibrium distribution, toward which the process moves. But note -- they aren't the same distribution in the two cases. Natural selection has a dramatic effect on what the equilibrium distribution is. So the movement towards an equilibrium does not mean that natural selection is ineffective.

I will be interested in seeing whether Mark Champneys agrees with this. His video gives the distinct impression that both cases are expected to have the same equilibrium distribution, with natural selection therefore being ineffective. That would seem to require some changes in the video, and some acknowledgement that maybe evolutionary biologists are not quite as ignorant of science as Mark Champneys said they were.