Genetic Algorithms for Uncommonly Dense Software Engineers
As promised, hot off the presses, here is a little tutorial I’ve decided to call Genetic Algorithms for Uncommonly Dense Software Engineers. Given some of the bizarre commentary issuing from the ID community over at Uncommon Descent regarding my past posts on Genetic Algorithms, I’ve developed this guide to help the folks over there figure out if the Genetic Algorithms (GAs) they are working on employ a “fixed-target” approach (like Dawkins’s Weasel), or if they are instead un-targeted, like most GAs used in research and industry are.

Background - the War of the Weasels For those readers wondering what this is all about, here’s a quick road-map to the key battles in this summer’s “War of the Weasels.”
Target? TARGET? We don’t need no stinkin’ Target! (Dave Thomas, July 5th, 2006) UDSE Response (scordova, July 9th, 2006) UDSE Response (scordova, July 14th, 2006)
Take the Design Challenge! (Dave Thomas, August 14, 2006) Tautologies and Theatrics (part 2): Dave Thomas’s Panda Food (scordova, Aug. 15th, 2006)
Calling ID’s Bluff, Calling ID’s Bluff (Dave Thomas, August 16th, 2006) Dave Thomas says, “Cordova’s algorithm is remarkable” (scordova, August 17th, 2006)
Antievolution Objections to Evolutionary Computation (Wesley R. Elsberry, August 18th, 2006)
Design Challenge Results: “Evolution is Smarter than You Are” (Dave Thomas, August 21st, 2006) Congratulations Dave Thomas! (davescot, August 22nd, 2006) Can humans compute better than computers? Dave Thomas’s design challenge (scordova, August 22nd, 2006)
Chapter 1: Check That Random Seed It may surprise some Uncommonly Dense Software Engineers (UDSEs) that the “random” numbers generated by compilers like C or C++ are not truly “random.” Rather, they are pseudo-random numbers, generated by an elaborate algorithm that uses a deterministic formula. These pseudo-random generators are usually initialized with the “seed,” a whole number that serves to start the deterministic formula off in a different place, leading to different “random” numbers.
If this seed is a constant, such as Zero (0), then the sequence of pseudo-random numbers will be exactly the same every time the program is run.
Of course, with this bad programming practice, there is no way the UDSE could determine if a given GA is targeted or not, because, even if it was not targeted, the result would always be the same.
Here is an example of this “no-no” in a supposed GA, scordova’s ga.c listing.
As another example, consider the use of a non-targeted algorithm, the Steiner GA, for a 5-node problem. Here, the seed for the random generator has been changed from something associated with the actual time of day to a constant, 0. As can be seen, the results of several generations (1000 here) always turn out the same. Everything turns out the same - the locations of every node, the connections between every pair of points, everything!
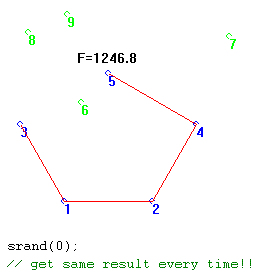
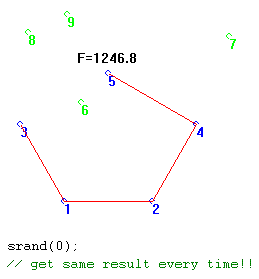
When the Seed is tied to time of day, however, the results of each trial of 1000 generations can be quite different, as shown in the following two trials.
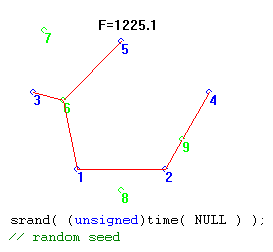
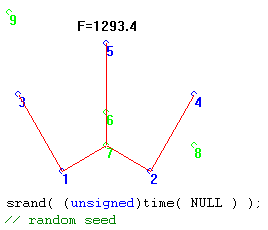
Chapter 1 Summary: Change the Random Generator’s Seed Every Time.
Chapter 2: Is the Answer Always the Same?
If the random generator seed is properly initialized so that the sequence of “random” numbers is different every time, the next step is to run the GA several times, and see if the Answer comes out the same every time.
For example, if if the random seed in ga.c is changed, the result is always the same - the sum of the first 1000 integers is always computed as 500,500. Similarly, the result of running Dawkins “Weasel” algorithm is always the same phrase, “METHINKS IT IS LIKE A WEASEL.”
To illustrate what a real (un-targeted) GA looks like when it is switched over to look for a fixed Target, I added a special feature to my Steiner GA to calculate fitness in a different way from the usual method, where Fitness is simply the length of all segments of a particular candidate solution.
When the “Target” button is checked, the Fitness Test is changed from its normal length calculation to the number of “DNA differences” between candidates and a specific organism (represented as a String in the GA). I could have selected the actual Steiner Solution for the 5-point problem, but decided instead to make the “Target” a rather inelegant and overly long candidate far from the actual answer to the 5-point problem.

Instead of selecting based on proximity to a target phrase like “METHINKS IT IS LIKE A WEASEL,” when the Steiner GA is run in Target Mode, it selects based on proximity to the string for the 2874-unit-long Kluge, target = “04614580132412507588758509TFFTFTFFTFFTFFTFFFFTFFFFFTTFFFFTTFFF”; // the Kluge
In subsequent runs, the Target is obtained every time. Here are two such runs; the first is an exact match to the Target (Fitness = number of DNA differences = 0), and in the second, the algorithm didn’t run quite long enough to get a perfect match to the Target, leaving it with a Fitness of 1. It certainly will achieve the precise target given more generations, however.
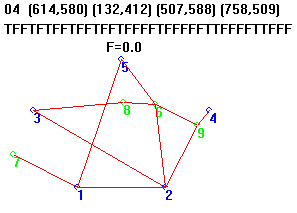
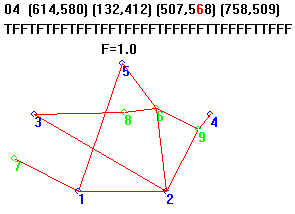
In summary, when a Fixed Target is employed, the GA converges to that Target every time it is run. Not surprising, actually!
Chapter 3: Is it just that Computers are Faster?
In his August 22nd response, Salvador Cordova of UD wrote the following:
Dave Thomas wrote:What is it going to be like having to go to Bill Dembksi and admit that you’ve learned the hard way of the true meaning of what Daniel Dennett terms Leslie Orgel’s Second Law: “Evolution is smarter than you are”?
Thomas has proven no such thing, neither Dennett nor Orgel. Computers can compute certain things faster than us, that is why they exist to help us. For Thomas to argue that evolution is smarter than humans because computers can compute faster than humans is a non-sequitur.
This appears to be the Final Retreat of Intelligent Design theorists. Recall that they originally said that GA’s work only because the Answer is fed into the GA via the Fitness Test. But, given a problem with no obvious answer, and one for which a Genetic Algorithm actually out-performed ID theorist Cordova, the fall-back position is “But Computers are FASTER than humans!”
Unfortunately, the Problem Space for the 6-point Steiner Grid is incredibly large. Using the basic points+segments data structure, there are billions upon billions of different possible solutions.
I set up my GA to also look at completely random solutions for a long time. When the normal GA runs, it can complete 1000 generations (one evolutionary simulation) in a couple of minutes. It works out to examining about 8000 individual solutions every second. On the overnight run leading to the Design Challenge, the Steiner GA found one actual solution after 8 hours (Simulation #150), and found the other (different handedness) solution just 39 minutes later (Simulation #162). In the 300 Simulations of the overnight run, the very worst result had a length of 1877, or about 18% longer than the actual Steiner solution’s length (1586.5 units).
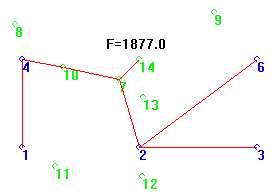
Compare that to simply running one mindless random solution after another, at 8000 solutions per second. Here is the best result obtained in 14 hours from over 400 million individual solutions. This has a length of 2502 units, almost 58% longer than the formal 6-point Steiner solution (1586.5 units).
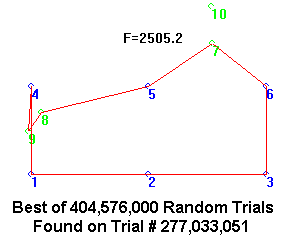
Of course, many of our human Intelligent Designers answering the Design Challenge got the formal Steiner solution in much less time than 14 hours. Just because a computer is “fast” doesn’t make it “smart.”
Genetic Algorithms don’t find useful and innovative solutions because they are “fast.” They do so because they are using the processes of selection, mutation and reproduction to solve problems, just as happens in Nature. And because the process is essentially unguided, it might not go down the wrong roads taken by human designers who have biases about what the solutions should look like. GA’s actually evolve new information in very reasonable times.
Sure, computers can perform faster than humans at some tasks. But even blinding speed is of little use when searches are random. It is evolution’s combining of random processes like mutation with deterministic processes like selection and reproduction that enable it to be “smarter than you are.”
RESOURCES
Make your own ‘Dummiez’ Book Covers!
