Design Challenge Results: "Evolution is Smarter than You Are"
They came for a contest that might someday be viewed as a pivotal moment in the eternal conflict between Darwin and Design.
On one side were the Intelligent Designers. They came from California and Alabama, New Mexico and England, Finland and the Netherlands, and from all around the world. They came from academia, and from industry, and from the armed services. They came armed with computer spreadsheets, home-made programs, graph paper and calculators. They applied trigonometry and calculus, intuition and insight, knowledge of minimal soap films and surface tension, database optimizing algorithms and random searches, and other techniques available only to Intelligent Designers. And they strived to answer the tricky question “What is the Steiner Tree (smallest possible network of straight line segments connecting six given points) for the network shown in “Take the Design Challenge!”
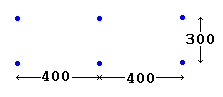
On the other side were Evolutionary (or Genetic) Algorithms, in which herds of digital organisms were bred over many generations. Each organism was a string of numbers and letters, which were “transcribed” by fixed rules as representing some of the billions upon billions of possible candidate networks for the given problem. Those organisms whose lengths were smaller gained a slightly better chance at being a parent of one of the organisms of the next generation, and mutations of the strings were allowed to happen occasionally. In this process, no trigonometry or calculus was required. No information about characteristics of Steiner Trees was necessary. But, as the strings competed with each other, marvelous and unexpected designs began to appear.
Although most of the Intelligent Designers were not members of the “Intelligent Design” movement, which had been officially invited to respond, the ID community did indeed weigh in, via the efforts of Salvador Cordova, one of the IDers running the show at William Dembski’s blog Uncommon Descent.
So, what is the Answer? Did Salvador do better than Darwin? Did our team of Intelligent Designers find the True Steiner, or did they, like the evolutionary algorithm, find “MacGyver” (not-quite-perfect-but-extremely-functional) solutions also?
Readers, let’s enter the Design Room and meet our Winners!
Let’s waste no time in meeting some of the entries that were closest to the actual Steiner Tree for the given six points.
One of these was generated by an assistant professor of mathematics and computer science at a major state university, and the other was generated by the Genetic Algorithm I discussed back in July.
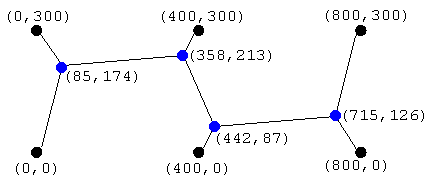
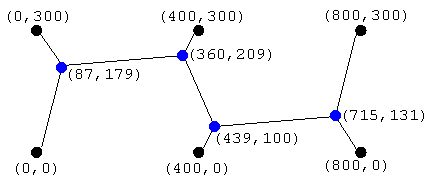
The interesting question now is, how can the Intelligently Designed answer be distinguished from the Evolved answer? Neither design is the exact Steiner solution, because one of our Designers might have rounded off too soon in his calculation, or perhaps mis-typed something somewhere along the line. If someone had access to the exact solution, they might be tempted to rule anything else out as “not designed.” But that’s not fair, according to Jonathan Wells’s new book, The Pig Ignorant Guide Politically Incorrect Guide to Darwinism and Intelligent Design, where on page 87 (Chapter 8), Wells writes
Nor does intelligence imply perfection. Some Darwinists criticize intelligent design on the grounds that some features of the natural world could have been made better. In other words, they argue that if something is not optimal, it is not designed. But things can be designed without being optimally designed. An automobile that is constructed in such a way that its fuel tank explodes whenever another vehicle bumps it from behind is badly designed, but it is designed nevertheless.
Before moving on to our other Winners, I’m issuing a Second Challenge, again open to all: using whatever ID theory you need (Explanatory Filter, Design Inference, whatever), show how this theory can be applied to the above two solutions to determine which was actually designed (e.g. “real” Complex Specified Information (CSI)), and which was evolved (and thus in possession of only the “appearance” of CSI).
Anyone can enter, but unlike the previous challenge, all contestants are asked to show their work. Again, e-mail your responses me at nmsrdaveATswcp.com (please replace the AT with an @), and do not post them as comments on this or other blogs. This new contest will be open for as long as needed (i.e. until the ID community makes a formal response), as it might take a couple of years for the top ID theorists to crack the case.
Let’s move on to the the Hall of Fame, and see what our industrious, hard-working Intelligent Designers came up with. It turns out that there are actually two perfect Steiner Trees possible: in one, the hexagonal grid is twisted counter-clockwise, and in the other, clockwise. Both Steiner Solutions are rotationally symmetric: like the Queen of Spades, they look the same if you spin them by 180 degrees. In addition to finding both of these solutions, the Genetic Algorithm (GA) production run I completed before issuing the challenge (300 simulations of populations of 1000 competing for 2000 generations each) found numerous other shapes, ten of which I’ve collected as official “MacGyver” solutions. I’ve tried to pick the MacGyvers to represent the various topologies (shapes) possible, but may have missed some. Many of our Intelligent Designers independently derived MacGyver solutions. Almost all of these were also found in the evolutionary simulation (the only ones not so appearing involved the overall shape above, but with flat horizontal segments instead of tilted ones). Interestingly, the Genetic Algorithm managed to find some interesting designs overlooked by all of the human contestants.
And the Winners Are… Please - if I’ve made any mistakes in the following, do let me know and I’ll make corrections. There were so many entries, it became hard to keep track of them all!
The Exact Steiner Tree
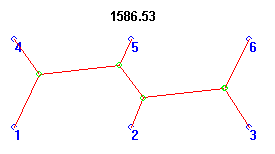
Kudos to George Atkinson, Bram de Beer, Paul Flocken, Virgil Keys, Alex Labram, Mike McCants, Ray Spurlin and Kim Van der Linde for nailing it, and showing us that the answer to this tricky problem can indeed be obtained via Intelligent Design!
All of these contestants came up with answers at or very close to the actual minimum length, 1586.53 units.
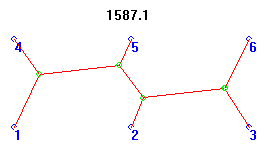
Congrats also to Kari Tikkanen for getting very close with the basic network, but with horizontal lines for the two long sideways-going segments; this length is also excellent (about 1591 units). Paul Flocken also designed this answer, but also kept after it until he acheived the true Steiner above.
Congrats also to those who simply visualized what the solution should be, qualitatively. That’s actually the hardest part of the problem, and kudos go to Bryan, Wes Elsberry, Dave Havlicek, Myron Souris, and Roy Thearle.
Additionally, Julian Onions also found the true Steiner, but did so with his own home-brewed Genetic Algorithm, thus providing independent confirmation that evolutionary processes can produce Designs.
While several Intelligent Designers found one or the other Steiner, it’s of interest to note the Genetic Algorithm found both.
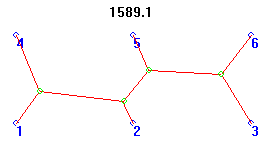
First MacGyver
 My first calculations for this curious shape led me to think it was the Second MacGyver, when in fact it was the First. My apologies to those contestants whom I confused with this error.
My first calculations for this curious shape led me to think it was the Second MacGyver, when in fact it was the First. My apologies to those contestants whom I confused with this error.
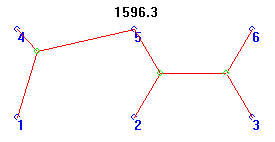
Kudos for finding this solution go to Roy Thearle, Ray Spurlin, Duncan Buell, Kevin Vicklund, Matthew Vonk, and Salvador Cordova (our official IDM respondent). At a length of 1596.3 units, this shape is only 0.6% longer than the formal Steiner solution!
It is of interest to note that Salvador’s first response was simply a drive-by URL drop on August 15, 2006 at 08:59 AM. Then, Salvador derived the “double bowtie” (Tenth MacGyver) over at UD on August 15, 2006 at 6:31 pm.
Cordova found a qualitative version of the above solution (First MacGyver), at UD on August 15, 2006 at 11:12 pm. After four more days of effort, Sal finally achieved the First MacGyver (and all four versions, too) at UD on August 19, 2006 at 5:04 pm.
While I appreciate his participation, this of course leads to some interesting new questions for Mr. Cordova. The first is, why did Salvador go the conventional route, finding web pages that discussed Steiner Trees or Fermat Points, and using trigonometry and algebra, like our other Designers? Why didn’t Salvador instead simply go get the answer from the Fortran listing of my genetic algorithm, as he said he could do in his Panda Food post:
Here is one of the many places where Dave sneaks the answer in: Dave Thomas’s Code Bluff
This is especially ironic because Cordova claims that my Steiner GA is just “theatrics,” and equivalent to his so-called “Genetic Algorithm” for summing integers. Although Salvador insisted that “The solution was never explicitly stored anywhere” in his summing algorithm, I was able to show exactly how Cordova “front-loaded” his algorithm with the specific solution desired. I did not simply go out and look up the formula N(N+1)/2 in a book - I reverse engineered Cordova’s Code to see how his answer was sneaked in. So, if I’m sneaking in the answer(s) with the Steiner GA, exactly where is that front-loading being performed?
Another question. Salvador, if we gave you a tee shirt with a bullseye on it, and told you to wear it so that you could find and shoot yourself in a game of paintball, would you be still be able to hit the Target?
My last question for Mr. Cordova is: what is it going to be like having to go to Bill Dembksi and admit that you’ve learned the hard way of the true meaning of what Daniel Dennett terms Leslie Orgel’s Second Law: “Evolution is smarter than you are”? Even after a week’s worth of effort, you still couldn’t find the correct Answer. You were close, but it’s Charlie Darwin (along with some very Intelligent Designers) who got the cigar. I predict there’ll be some ‘splainin’ to do backstage at Uncommon Descent.
Second MacGyver
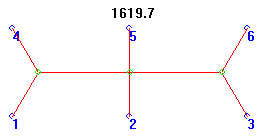
Unlike the First MacGyver, the Second MacGyver has eye-pleasing symmetry, and was engineered by several of our industrious Intelligent Designers. At a length of 1619.7 units, it is but 2.1% longer than the optimal Tree. Kudos to Ron Bear, Matt Brauer, Duncan Buell, Reed Cartwright, Otto Froehlich, I.R. Pen, John Shipman, Lance Stewart, and Kevin Vicklund..
Third MacGyver
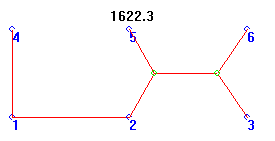 Only Darwinian processes found this optimal form of curious shape, weighing in at around 2.3% longer than the formal Steiner. However, Andrew McClure ran a Random Search algorithm for 24 hours, and found a topologically-correct (but severely distorted) version of the Third MacGyver on the 3,191,313th iteration.
Only Darwinian processes found this optimal form of curious shape, weighing in at around 2.3% longer than the formal Steiner. However, Andrew McClure ran a Random Search algorithm for 24 hours, and found a topologically-correct (but severely distorted) version of the Third MacGyver on the 3,191,313th iteration.
Fourth MacGyver
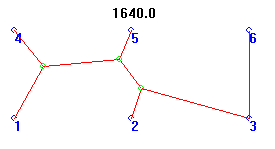 Again, only the Genetic Algorithm found this odd shape, coming in at 3.4% longer than the best solution.
Again, only the Genetic Algorithm found this odd shape, coming in at 3.4% longer than the best solution.
Fiifth MacGyver
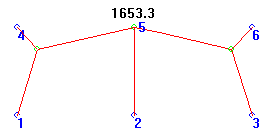 This pretty bilaterally-symmetric design was found by the GA, and also by Kevin Vicklund, and is 4.2% longer than the ideal tree.
This pretty bilaterally-symmetric design was found by the GA, and also by Kevin Vicklund, and is 4.2% longer than the ideal tree.
Sixth MacGyver
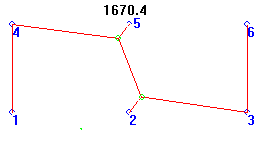 Only the GA found this artistic rotationally-symmetric shape, at 5.3% longer than the official solution.
Only the GA found this artistic rotationally-symmetric shape, at 5.3% longer than the official solution.
Seventh MacGyver
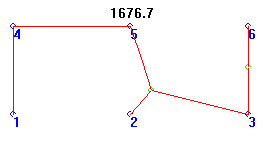 Again, only the GA found this odd shape, at 5.7% longer than the optimum.
Again, only the GA found this odd shape, at 5.7% longer than the optimum.
Eighth MacGyver
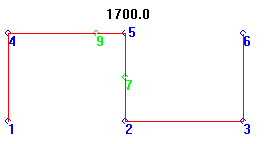 This solution was derived by Reed Cartwright and Kevin Vicklund, and is 7.2% longer than the formal answer. There are several equivalent networks, forming an M or W instead of an S, and all with length 1700. A horizontal line through three verticals would also yield the same length (kudos Kim Johnson. Many of these fit the “Traveling Salesman Problem” class of solutions (i.e. having no internal “Steiner Points” for making connections).
This solution was derived by Reed Cartwright and Kevin Vicklund, and is 7.2% longer than the formal answer. There are several equivalent networks, forming an M or W instead of an S, and all with length 1700. A horizontal line through three verticals would also yield the same length (kudos Kim Johnson. Many of these fit the “Traveling Salesman Problem” class of solutions (i.e. having no internal “Steiner Points” for making connections).
Ninth MacGyver
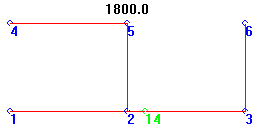
Again, only the GA found this curious tree, at 13.5% longer than the Steiner.
Tenth MacGyver
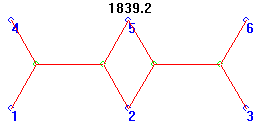
This elegant design was found by Kevin Vicklund, who, while not getting the Steiner itself, is commended for finding five different MacGyvers. Evolution may be smarter than Kevin, but Kevin is doing a great job catching up, and is hereby named the Master of MacGyvers for this contest! Credit also to Salvador Cordova for finding this shape as his first serious attempt, as was mentioned previously.
I got into the six-point problem by trying to find the network that could produce the Double Bowtie as its Steiner Solution. Without giving the matter a great deal of thought, I started a simulation to look at the six-point problem, figuring that I might get lucky and snag a Double Bowtie or two from the run. But, when I sat down to review the solutions, the Double Bowtie was nowhere in sight. In fact, to get the image of the Double Bowtie shown above, I had to deduce its DNA pattern and feed it directly into my plotter routine. I had to chuckle at myself when I realized that at 1839.2 units in length (almost 16% longer than the optimal solution), the Double Bowtie would always be out-competed by shorter, tougher MacGyvers.
However, looking over the simulation results, I noticed that the best answers indeed came from a mutated version of the Double Bowtie, in which the four segments connecting the middle two points (2 and 5) could be replaced by only three segments in the shape of a dog-leg, and that this could be realized by tilting both Bowties at a slight angle, either clockwise or counter-clockwise. And so I learned that Evolution is smarter than me, too. Once I stopped chuckling, I realized that this was an excellent example of a problem with no obvious answer, and a good candidate for the Design Challenge, which followed shortly thereafter.
Honorable Mention
Kim Johnson derived “The Asterisk,” in which two long diagonals and one vertical all meet in the center of the figure, forming an asterisk shape. This has length 2009 units.
And Rupert Morrish sent in this whimsical answer:
CONCLUSION
In The Pig Ignorant Guide Politically Incorrect Guide to Darwinism and Intelligent Design, Wells writes
Ferry passengers entering Victoria Harbor in Canada are greeted by a bank covered with flowers that spell out “WELCOME TO VICTORIA” in large letters. Everyone who sees the greeting knows immediately that it was intelligently designed.
Likewise, anyone who comes across one of the Steiner or MacGyver designs shown in the Design Room would probably infer design, especially if they knew of the effort required to derive such designs. But, given that these “designs” can also be found simply by breeding herds of alphanumeric strings, it becomes clear that evolutionary processes can also produce the appearance of design.
To those Designers who found “MacGyvers” instead of the official Solution - pat yourself on the back. You have helped to show that the McGyver solutions are Complex Specified Information in their own right.
Expect to see more of the typical ID/creationist reactions to these results. We will hear (again) that the GA won’t run if program lines are switched or mangled randomly, as if this means anything. I mean, really - if all the oxygen atoms in the world were suddenly replaced with sulphur atoms, wouldn’t Life cease immediately? And the point is…?
When I showed this algorithm to William Dembski in 2001, he dismissed it as mere “frontloading” of the answer via the GA’s fitness function. But what such “frontloading” really entails is the erroneous belief that simply Asking a Question is sufficient to produce the Answer. We all know from personal experience that not all Questions have obvious Answers.
And, we’ve learned this past week that answers to the question “What is the Steiner Tree for a given network?” are anything but obvious. Thanks to all of the many contest participants who sent in their designs. You have participated in a unique experiment that puts Darwin and Design to the test under precisely controlled conditions. I appreciate and applaud your earnest efforts!
P.S. Contestants, if you are feeling a need for some new puzzles to engage the ol’ brainpan, check out the Pirate Chest Challenge over at NMSR.
